|
| Command: |
Preprocessing > Correction to an Internal Standard |
Sometimes it is necessary to calibrate the measured spectra to an internal standard (this can be helpful, for example, if the overall intensity of an image degrades from top to bottom because the data acquisition took too long and the sample degraded during measurement). In this case it is a good idea to add an internal standard which can be used for an intensity correction of the pixels (cf. [Bonta 2014a]).
One particular problem of internal standards is the noise of the standard data which may introduce additional noise into the processed layers. Epina ImageLab addresses this problem by averaging the standard layers (if more than one layer is selected as a standard). Optionally, the standard layer(s) may be smoothed by a spatial filter to reduce noise even more. The operating window of the spatial filter is quadratic with an edge length twice the "spatial smoothing range" parameter. Please keep in mind that the spatial filter may blur the visible structures in the processed layers if the smoothing window is greater than the corresponding structures.
If you want to exclude parts of the image from standardisation you can defined a pixel mask and select this mask with the control "Pixels not to process".
| How To: |
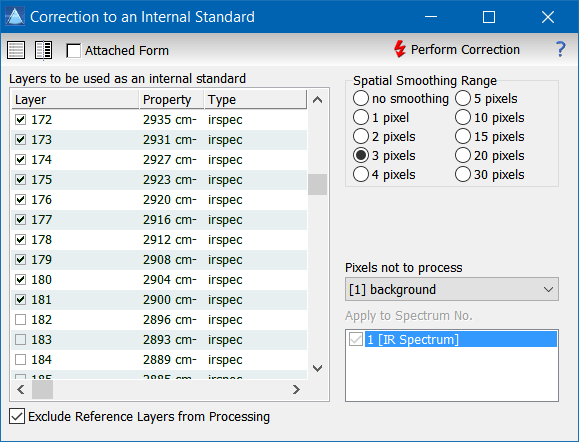
Please follow these steps to rescale your data to an internal standard:
- Select the layer(s) to be used as an internal standard. If several layers are selected, the mean of the selected layers is used as the internal standard (this might be useful, for example, when several isotopes of the same element have been measured as an internal standard).
- Select the spatial smoothing. This defines the range around each pixel which will be used for the calculation of the reference value. A non-zero value may be helpful if the internal standard layer is in principle uniform and there are only noise related variations from pixel to pixel.
- Click "Perform Correction"
|
| Hint: |
Please keep in mind that the correction to an internal standard can require considerable computing time if the spatial filter is set to its maximum (30 pixels smoothing range). For example, a hyperspectral dataset consisting of 500 by 500 pixels, with each spectrum resolved to 360 intensity entries results in 500x500x360*(2*30+1)2 = 334.9 billion summing and matrix addressing operations - which will take about half an hour on an average computer. |
|
Tools 
