|
The function EstimateParaboloid calculates a parabolic/hyperbolic regression surface for a dataset given by the matrix InData and writes the estimated surface values into the matrix OutData. The function can be any mixture of a parabolic and a hyperbolic surface. The array OutData is automatically resized to match InData. This routine can be used, for example, to neutralize the data of tilted surfaces showing a systematic change of sensitivity across the entire image.
The parameter NSample controls how many pivot points are used for the calculation of the parabolic model. You can either use a regular raster of pivot points or randomly selected positions. A negative NSample value results in random sampling, a positive value results in NSample evenly spaced pivot points. Setting NSample to zero uses all pixels of InData (this may take considerable time if the matrix InData is large). In general, sampling about 1000 points is sufficient for most purposes. If the array InData has less cells than NSample, all cells are used as pivot points.
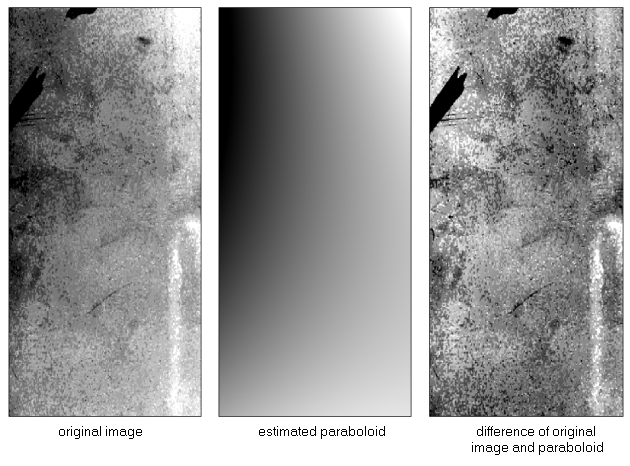
The following example shows an image which exhibits an underlying trend: the left part of the image is darker than the right part, especially the corners (left), if one subtracts the modelled paraboloid (center) from the image, the resulting image shows a higher contrast. The uneven intensity in this image came from a circular non-centric light source.
The function returns the following error codes:
0 ... everything is OK, OutData has been filled by the estimated values
-1 ... the model cannot be calculated (due to numerical problems)
|
Script Language 
